网络安全检测|网络安全服务|网络安全扫描-香港墨客投资移动版

　　看这是多么简单的知识与真理，请不要再觉得这很难，那些复杂的计算过程与你有半毛钱关系吗？你要做的事情就是理解这些数字在向你诉说的秘密而已。

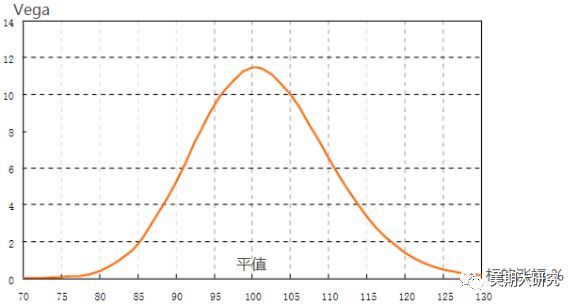
　　图4：Vega与标的价格的变化图

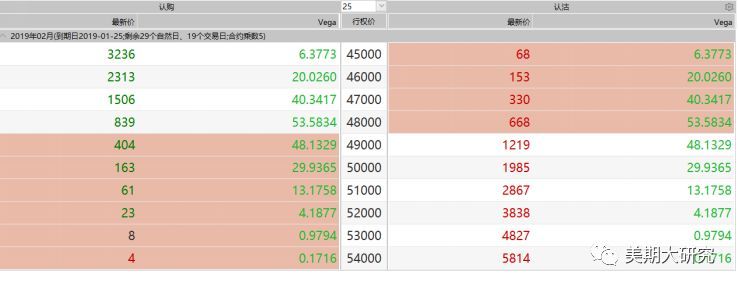
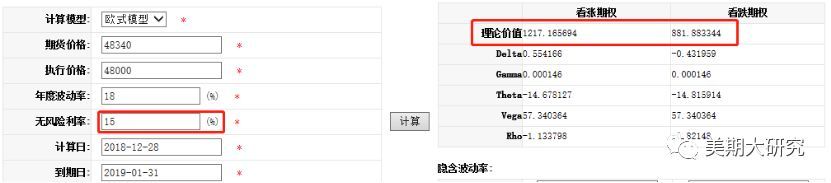
　　用一个简单的例子来简单阐述Vega所代表的含义。

　　它度量了期权价格对波动率变化的敏感性。以下是以837的价格买入Cu1902-C-48000,我们可以发现此时头寸的Vega值为53.1，当前的隐含波动率为14%,如果波动率上升1%,理论上期权的价格将上涨53.1元，变为890.1，如果波动率下降1%，那么期权的理论价格将下降53.1元，变为783.9元。这样理解起来似乎也很简单呀。

　　波动率的变化对期权价格的变化是特别重要的，尤其是在处于平值期权的时候。如果细心的交易者会发现，即使我们很多时候标的的价格没有发生实质性的变化，维持了很长时间的盘整，然而期权的价格却发生了较大的变化，依然会让你获利。这里的获利逻辑就是波动率发生了变化，即使内涵价值没有太大变化，但只要盘中波动率会发生改变，只要波动率增加足够多，且足以抵消时间价值的衰减，那期权价格同样会大幅上涨。

　　四、 期权价格随时间变化的敏感性—Theta

　　时间价值的侵蚀是我们在期权交易中需要重点考虑的问题。我们常说时间是期权买方最大的敌人，每时每刻时间都在吞噬着期权的价值，时间是期权卖方的伙伴，卖方一点点的赚取时间消耗带来的利润。Theta可以来描述期权价值随时间的变化情况。用Theta衡量的是随着存续期的减少，期权价格的变化大小。从数学上来说，它是期权价格关于时间t的导数。还是从软件的显示上来直观的感受一下Theta的变化情况。

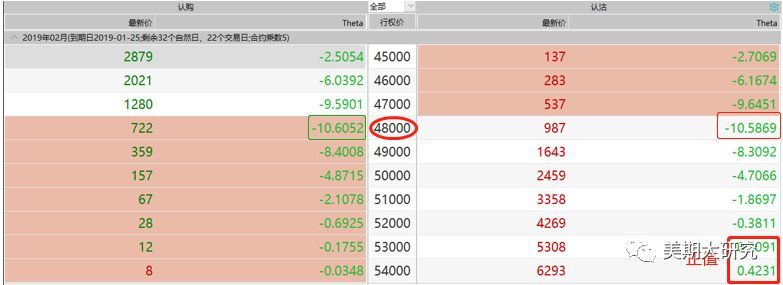
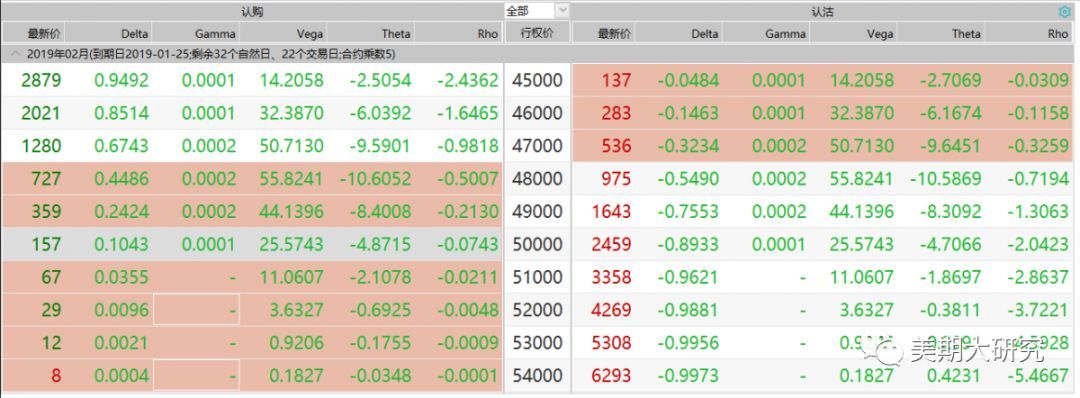
　　图的解释：Theta值貌似均为负值，但在右下角又出现了两个正值。按照常理来说，随着时间的消失，期权价值是在不断减小的，所以Theta应该均为负。出现正值的情况的归因于利率的贬值效应，这样的情况存在，但是少见，我们在此不给予考虑这种极端情形，默认Theta都为负值，在平值期权位置时，Theta值最大，预示着时间的衰减是最迅速的，面对时间的变化反应是最灵敏的，当期权处于极度虚值和实值时Theta会变得很小，也表明在实值和虚值状态时，期权价值对时间变化的敏感度比较迟钝。当然这只一个静态的描述，我们并没有从动态的角度来解释它的变化过程。在这里多补充一点，Theta的变化并不是一个线性的，期权时间价值的随时间的变化更像是分阶段的，随着到期日的临近，衰减速度在不断的加快。大约可以从下图来描绘这种变化规律。

　　举例说明Theta的含义

　　这是以925元买入Cu1902-C-48000，头寸的Theta值为-18.45，这就意味着期权的时间过去一天，期权的价值就损失掉18.45。当然这样的说法仅仅是停留在静态下，在过两天Theta值可能已经远远超过这个值，而且越临近到期日，这个值会变得越大。

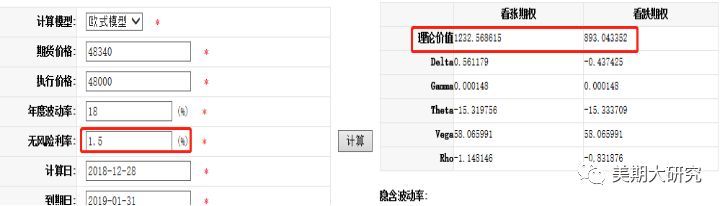
　　五、 期权价格随利率变化的敏感性—Rho

　　Rho衡量的期权的价格随利率的变化情况。此风险的度量指标与以上四个指标比起来就显得不那么重要了。为什么这样说，一是从利率的变化来说，利率的变化一般不会很大，长期会保持一个稳定状态；其二是，就算变化很大，对期权价格的影响也是非常有限的。不妨来演示一下。

　　当利率为1.5%时和利率15%时期权的价格变化非常小，在利率变化10倍的时候才发生一些细微的差距，而在现实中理论按照10倍量级变化的情况。另外利率对期权价格变化的分析又十分复杂，投入与产出出现明显的失衡，罢了，不研究也罢。如果期权的持仓头寸很大，可以在利率的分析上下一些功夫，如果仓位比较小，还是不要浪费精力了。

　　六、总结

　　最后我们把我们所介绍的五个风险指标都放在一起。我们单独的分析了每个指标的变化特征，各自的含义以及应用的例子。