网络安全检测|网络安全服务|网络安全扫描-香港墨客投资移动版

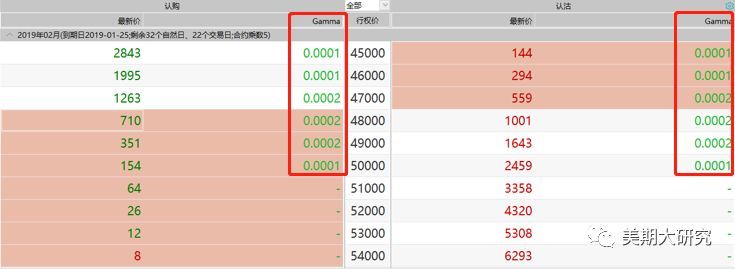
　　这个很好理解，期权的价格会随着其标的上变化而变化，只是其变化的速率和幅度和其标的存在一些差异，因为期权除了受标的的影响外还受到其他因素的影响，所以其有些特殊的属性。如果我们调整期权头寸使得其Delta为1，在理论上就等同于交易了期货头寸（但这不是真正意义上的等同），如果交易期权的时候存在优势，我们完全可以利用期权来构造一个等同期货的头寸。

　　第四种理解：Delta代表概率。

　　这种理解可以作为参考，这无法从严格的学术上说这种理解正确，可是在交易中确实有一定的实用性。Delta的绝对值大小，代表到期日时，期权变成实值期权的可能性大小。一旦期权变成实值期权，期权的买方就有可能行权，Delta从一定程度上反应了获利的概率，当然行权与否还得看实值期权的实值程度。

　　如果此时以2130买入CU1902-C-46000，这是交割单截图。

　　Delta=0.8348，大约可以理解为在期权到期日为实值期权的概率大约是83.48%，其实这个概率还是很高的，但是我会不会行权，以及我在行权中能否获利，还得考虑实值程度。如果不能覆盖掉权利金成本，是无法获利的。尽管这种理解和实用性没有太强的作用，但是作为参考，对我们的交易还是会有协助作用的。

　　二、 Delta关于期权价格变化的敏感性—Gamma

　　先直观的感受一下Gamma。如下图

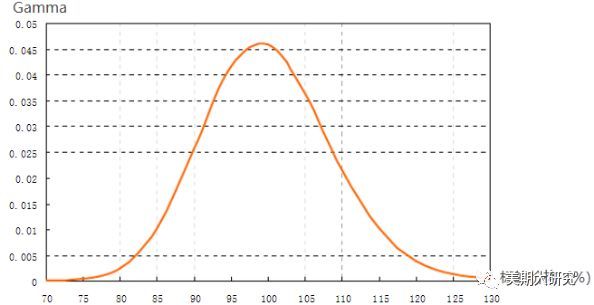
　　你会发现，在相同的执行价上看涨期权和看跌期权的Gamma值相同，而且所有的Gamma值均为正值。仿佛从直观上也就只能得出这些结论。简单的归纳以下Gamma的特征，重点还是讲其所代表的含义和其运用。

　　图3：Gamma值与标的价格关系

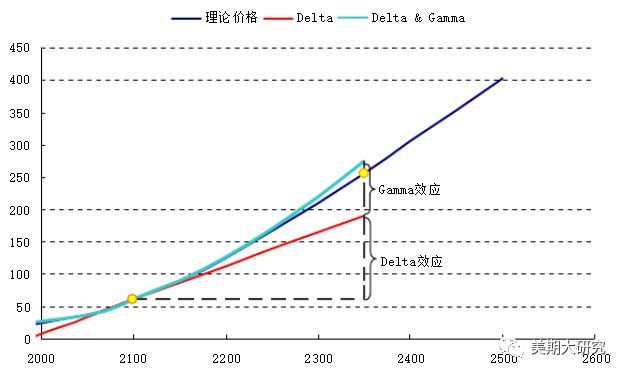
　　看涨期权和看跌期权的Gamma值是一样的，从上图可以看出，平值期权附近Gamma值最大，而当期权处于极度实值和极度虚值Gamma都趋近于0。这一点很好理解，Gamma衡量的是Delta对期权价格变化的敏感性，在平值期权位置Delta的变化比较快，而在深度实值和虚值时Delta对价格变化显得比较迟钝。高Gamma值都意味着高风险，而低Gamma意味着较低的风险水平。

　　Gamma对期权价格的影响是间接性的。Gamma通过影响Delta的变化来影响期权价格的变化。如果我们忽视其他因素的影响，我们可以简单理解成是Delta效应和Gamma效应来影响着期权理论价格的变化。这里简单的提一下，为后来我们学习动态风险的控制具有非凡的意义。用一副图来直观的反应这两个效应基本情况。

　　举个例子说明。

　　之前我们在解释Delta对期权价格影响的时候，若Delta=0.8，说明标的价格每变化1，期权价格变化0.8，而这个Delta却是一个瞬时值，我们假定了这个值是不变化的，换句话说在当前这一刻Delta=0.8，那么下一个时刻会变成多少了？问题就出现在这里了，那么Gamma就可以来帮助回答这一问题，如果用△来代表Delta值，用Г来代替Gamma值。标的的初始价格为S0，变化到S1,在S0是期权的理论价值为C，如果我们要考虑得更加精细，我们考虑到Delta的变化，此时△=△+Г(S1-S0)，那么此时期权理论价格会变化为 C+(△+Г(S1-S0))(S1-S0)。

　　当然这是提供了一个新的思想，平时的计算也不会这样粗略，更多的时候会采用平均数来算。如果高中你是理科生，结合运动学的理论来理解Delta和Gamma的关系和我现在阐述的问题，你会觉得Gamma和加速度如出一辙。

　　多说无益，此处有个概念就好，知道在Delta和Gamma这两个风险指标很重要，尤其在平值期权附近时变化比较大，目前我们所说的都是静态的风险，如果考虑到动态风险问题又会变得复杂，这也是大头针风险难以管控的原由。

　　三、 期权价格关于波动率变化的敏感性—Vega

　　期权Vega值指波动率每变动一个百分点期权理论价值的变化。由于所有期权都会因为波动率增加而价值上升，所以看涨期权与看跌期权的Vega值均为正数。平值期权的vega值最大，而实质期权和虚值期权的较小。这也就意味着平值期权的价格对波动率的变化是最敏感的。

　　目前我们只是从静态的变化来分析的，并且也是敏感性分析。实际情况是，时间与波动率是紧密相连。更长的剩余到期时间意味着波动率有更多的时间产生影响，更短的剩余时间意味着任何的波动率只能对期权价值产生很小的作用。在很多时候剩余时间的变化和波动率的变化对期权价格产生相似的影响。在软件里Vega呈现得非常直观，Vega值均为正数，而且同一执行价下看涨期权和看跌期权Vega值一样。而且在平值期权处Vega最大，在向实值和虚值的变化过程中逐渐变小。