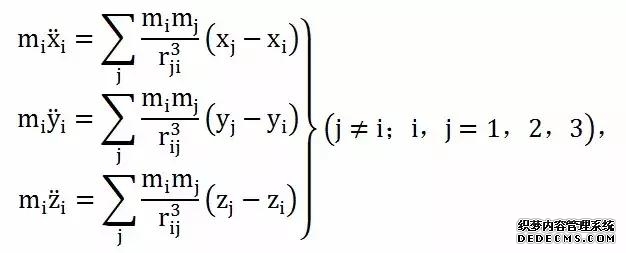网络安全检测|网络安全服务|网络安全扫描-香港墨客投资移动版

于是，三体问题中Q i的运动微分方程可以写为：

上式在直角坐标轴中的投影式为：

所以，三体问题中的每个天体在数学中都可以被写成3个二阶常微分方程，共6阶，三个天体就是18阶。

因为已知积分不足以解决三体问题，所以科学家们的研究方向，就是如何去简化数学式了。

著名数学家布伦斯和庞加莱曾证明n体问题只有10个运动积分，即3个动量积分，3个关于质心运动的积分，3个动量矩积分和1个能量积分，而且它们都是代数式。

应用这10个积分可将三体问题的18阶方程降低到8阶，再用“消去时间法”降低到7阶，又用“消去节线法”降低到6阶。如为平面三体问题则可降为4阶。

不过，消除了运动积分和时间、结线、维度的三体问题，只能被称为“理想状态”下的三体问题。

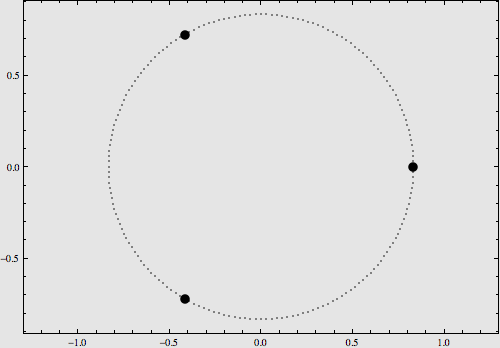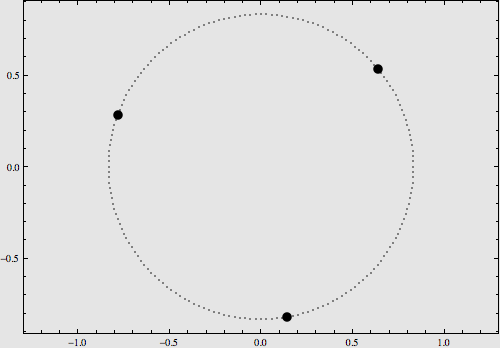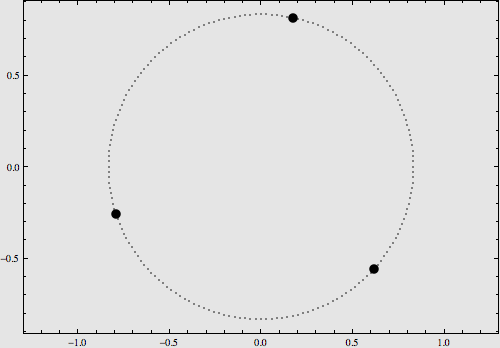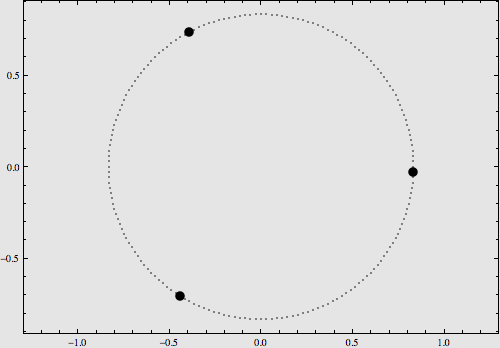
若想要解决完整的三体问题，所有的积分和条件就都需要考虑进来了，“理想状态”下的三体问题，只是给完整的三体问题指了一条明路。

三体问题的研究成果

在三体问题被提出后的两百年间，几乎所有18、19世纪的著名数学家都尝试过去求解，但研究进展微乎其微，直到希尔伯特那次著名的演讲，才终于有了突破。

这次三体问题的突破，主要是发现了三体运动的三种特殊情况，在这三种特殊情况下，三体问题具有特解。

1.拉格朗日-欧拉族：三星成三角形,围绕三角形中心旋转；

2.布鲁克-赫农族：两颗星围绕第三颗星旋转；

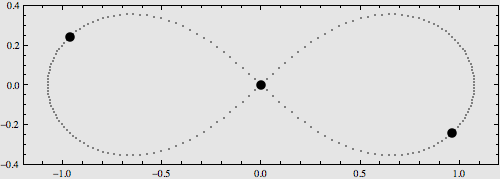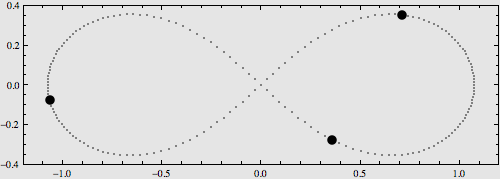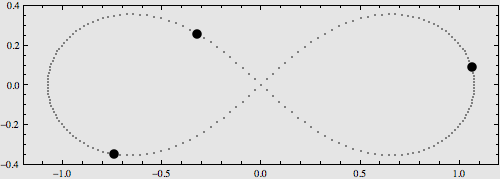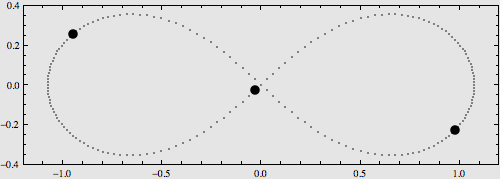
3. 8字型族：三个等质量的物体在一条8字形轨道上运动。

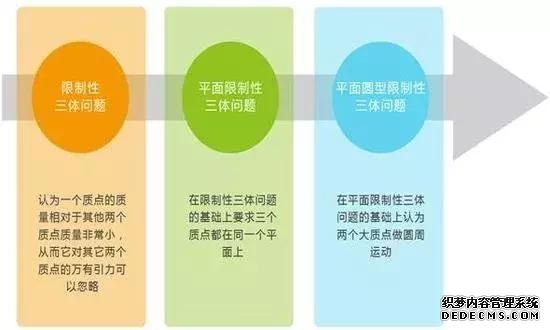
但同样，这也属于“理想状态”下三体问题的范畴，为了更直观解决三体问题，后来的科学家们还提出了“限制性三体问题”：

在限制性三体问题的条件下，三体运动已经是对实际物理简化得很厉害了，比如说对质点，球体自转、形状这些因素统统不考虑。

然而无论怎么变化，牛顿、拉格朗日、拉普拉斯、泊松、雅可比、庞加莱等等大师们，为这个问题穷尽精力，也未能将它攻克。

科学发展到现在，三体问题的求解过程真的是一部令人心酸的简化史。

虽然三体问题没有被最终攻克，但科学家们在研究过程中，取得了非常有用的成果。

1772年，拉格朗日在“平面限制性三体问题”的条件下找到了五组特解，从而发现了沿用至今的“拉格朗日点”。